
Studio One observes a shift in architectural practice from direct design, wherein specific design instances are produced largely through compositional strategies, to deferred design, wherein generalized systems of possible designs are generated through parametric strategies. Reflective of this shift is the concept of a "design space", or, the family of possible designs implied by a set of constraints and variable generative routines. Where compositional strategies are productive of unique instances for, say, the design of a piece of flatware, parametric strategies are generative of the entire flatware set, and imply design instances, parametric hybrids, perhaps unforeseen by the authors of such a system. Such a strategy abstracts the design process, thereby removing the author from direct manipulation of the product of her work, presenting both hazards and opportunities for creative production.
This short exercise offers a chance to explore the mechanics of deferred design through the design of simple object that, even in its conventional form, implies an untapped space of design instances - the chesspiece.
Select two pieces from the standard Staunton chess set, and one "fairy" chess piece from the list appearing on Wikipedia. The "fairy" piece will not hold a standard representation in the Staunton set, and must be designed. Model each of these in Rhino.
Produce a parametric model in Grasshopper of each of these pieces (separately), parameterized such that standard dimensions such as base width, height, etc may be adjusted. Control each of your chess pieces using exactly three parameters.
Produce a single parametric model in Grasshopper that, through the manipulation of exactly three parameters, produces an instance of one of the three standard pieces above, or a parametric hybrid of them.
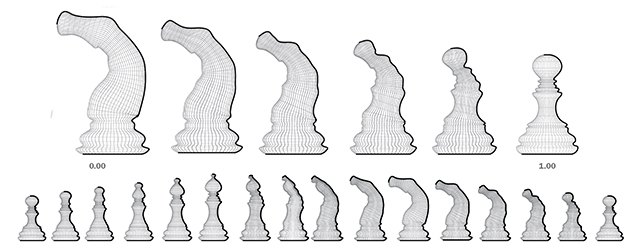
Prepare a graphic representation of the design space implied by the Grasshopper model produced in Step 3.
Your work in Part One has produced a design space of chesspieces - a single design with a multiplicity of incarnations. In part two, we will qualify this design space as a way of informing the selection of individuals within it.
Identify two qualitative properties (bigness, fatness, roundness, sharpness) of your chesspiece. As the properties you choose should reflect an aesthetic position on the object, and not merely a technical one, select properties that suggest aesthetic criteria, and not necessarily those that are easiest to quantify.
Continuing to work on the single parametric model produced in step A3, produce a quantification of each of the qualitative properties you've identified. These may be expressed as measures (such as area, circumference, curvature), ratios (area of largest cross-section to smallest), aggregations (average curvature, number of moments of very high curvature). Produce one printed drawing (18"x24", portrait) for each property that depicts design instances with extreme values of this property, and demonstrates the geometric method of quantification.
Using the Lemmings plugin, perform brute-force searches of your design space that identifies instances with both high and low values for the properties of interest. Produce one printed drawing (19"x24", portrait) that depicts the results of these searches and show at least 200 members of the design space. Each member should be notated with relevant information and graphics that indicate the geometric method of quantification. In addition, using the standard PNG ouput of Lemmings, produce an animation of the process of the design search (800x800px, white background).
Using the Galapagos plugin, perform a genetic algorithm search of your design space that identifies the same high and low values for the properties of interest. Produce a screen-shot animation (800x800px) of this process, and be prepared to discuss the relative merits of genetic searches vs. brute-force searches.
There's more!
Some other projects from this same class have been posted, as well as some interesting student work from this same year.